스테라디안(steradian)이란?
스테라디안(steradian)은 3차원 공간에서 어떤 점을 중심으로 펼쳐진 공간의 크기를 나타내는 단위입니다. 마치 평면에서 각도를 라디안으로 측정하듯, 입체적인 공간에서의 각도를 측정하는 데 사용됩니다. 아래의 그림에서 입체각이 떨어진 거리(x)의 제곱 대비하여 보이는 시야의 면적(A)의 비율로 표현이 되어 있는데 이러한 입체각의 단위를 스테라디안이라고 합니다.
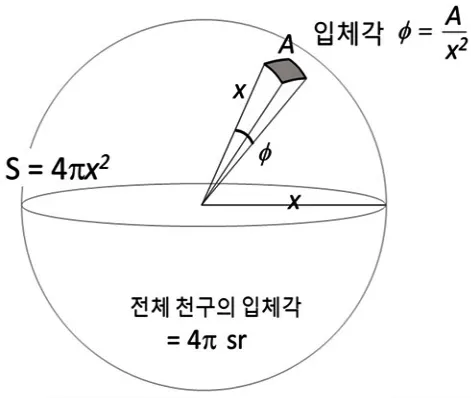
스테라디안의 정의
1 스테라디안은 어느 정도의 크기일까요?
반지름이 r인 구에서 r²의 면적을 차지하는 부분이 만들어내는 입체각이 1 스테라디안입니다. 쉽게 말해, 구의 중심에서 볼 때, 구의 표면에서 반지름의 제곱만큼의 넓이를 차지하는 부분이 만들어내는 시야각이 1 스테라디안(sr)인 것입니다.
위의 그림에서 이해한다면, x가 r이며, A가 r2인 경우가 바로 1 [sr] 입니다.
![1 [sr] 의 크기](https://blog.kakaocdn.net/dna/oDvJt/btsKqZckjcT/AAAAAAAAAAAAAAAAAAAAAOPsUgE6NScKo5gq2a3kYBg4pfQ_z1wmzX3LWMcWANKS/img.webp?credential=yqXZFxpELC7KVnFOS48ylbz2pIh7yKj8&expires=1772290799&allow_ip=&allow_referer=&signature=x%2FYiNO8djzhug4u0dSWmXkasFns%3D)
구 전체를 다 보는 시야각은 몇 sr일까요?
반지름인 r인 구의 표면적은 4πr2입니다. 따라서 구 전체를 다 보는 입체각은 4πr2/r2= 4π [sr]입니다. 여기서 좀 더 응용하자면, 우리가 반쪽인 구를 다 보는 시야각은 2π [sr] ~ 6.28 [sr] 의 크기라고 생각할 수 있습니다.
아래는 이해를 돕기위해 일상 생활에서의 스테라디안 값을 표현한 그림입니다.반쪽인 구의 표면적을 다 보는 입체각의 크기가 6.28 [sr]이라고 생각하면 그림에서 설명하는 상대적 크기를 이해하기 쉬울 것입니다.

왜 스테라디안이 필요할까요?
- 빛의 세기: 빛의 세기를 측정할 때, 광원에서 나오는 빛이 얼마나 넓은 공간에 퍼져나가는지를 나타내기 위해 스테라디안을 사용합니다.
- 안테나 성능: 안테나가 전파를 얼마나 넓은 범위로 보내거나 받을 수 있는지를 나타낼 때도 스테라디안을 사용합니다.
- 천문학: 별의 밝기를 측정하거나, 천체의 크기를 측정할 때도 스테라디안이 활용됩니다.
스테라디안과 라디안의 비교
| 특징 | 라디안 | 스테라디안 |
| 차원 | 2차원(평면) | 3차원(공간) |
| 정의 | 원의 반지름과 호의 길이를 이용한 각도 | 구의 반지름과 표면적을 이용한 입체각 |
| 단위 | rad [m/m] | sr [m2/m2] |
| 활용 분야 | 수학, 물리학 등 다양한 분야 | 광학, 천문학 등 |
스테라디안은 3차원 공간에서의 각도를 나타내는 단위로, 빛의 세기, 안테나 성능, 천문학 등 다양한 분야에서 활용됩니다.
라디안(radian)과 도(degree): 각도를 나타내는 두 가지 방법
'Learn > 과학공학기술' 카테고리의 다른 글
| 알파폴드: 단백질 구조 예측의 혁명 (0) | 2024.11.08 |
|---|---|
| 브레트 법칙: 유기화학의 기본 원리와 새로운 가능성 (0) | 2024.11.04 |
| 라디안(radian)과 도(degree): 각도를 나타내는 두 가지 방법 (1) | 2024.11.01 |
| 광학 두께(광학적 깊이, Optical depth)의 의미와 중요성 (0) | 2024.10.22 |
| 달의 같은 면만 보이는 이유: 조석고정(Tidal Locking) 쉽게 설명 (1) | 2024.10.17 |



