라디안과 도는 모두 각도의 크기를 나타내는 단위입니다. 하지만 각기 다른 방식으로 정의되고 사용되는 점이 있습니다.
라디안(radian)
정의
라디안은 원의 반지름과 같은 길이의 호가 중심각으로 만들 때의 그 각의 크기를 1라디안이라고 합니다. 즉, 원의 반지름을 r, 호의 길이를 l이라고 하면, 라디안(radian)은 다음과 같은 관계를 가집니다.
radian = l / r
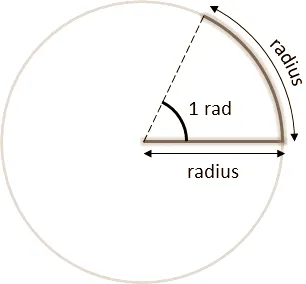
따라서, 호의 길이가 반지름과 같을 경우(l=r, 아래 그림 참조), 1 radian의 크기입니다.
radian = r/r = 1
특징
- 자연스러운 단위: 라디안은 길이(호)와 길이(반지름)의 비율이므로 무차원 단위입니다.
- 수학적 편리성: 삼각함수, 미적분 등 수학에서 라디안을 사용하면 공식이 간단해지고 계산이 편리합니다.
- 물리학에서의 활용: 원운동, 진동 등 물리학의 다양한 분야에서 라디안이 사용됩니다.
도(degree)
정의
원을 360등분했을 때 한 부분이 이루는 각을 1도라고 합니다.
특징
- 일상생활에서의 활용: 시계, 지도 등 우리 주변에서 흔히 사용되는 단위입니다.
- 직관적인 이해: 360도라는 숫자는 1년이 365일과 관련이 있을 뿐 아니라, 원의 특성을 고려한 역사적인 배경을 가지고 있습니다.
라디안과 도의 비교
| 특징 | 라디안(Radian) | 도(Degree) |
| 정의 | 원의 반지름과 호의 길이 비율 | 원을 360등분한 각 |
| 단위 | 무차원 | 도(°) |
| 수학적 특징 | 수학적 계산에 유리 | 직관적 이해가 쉽고 일상생활에서 많이 사용 |
| 주요 활용 분야 | 수학, 물리학 | 일상생활, 지리학 등 |
라디안과 도의 환산

라디안을 도로 변환
라디안에 180을 곱하고 π로 나눕니다. 도 = 라디안 × 180 / π
도를 라디안으로 변환
도에 π를 곱하고 180으로 나눕니다. 라디안 = 도 × π / 180
예시
1라디안은 약 57.3도입니다. 90도는 π/2 라디안입니다.
왜 라디안을 사용해야 할까요?
라디안은 수학적인 계산에서 더욱 자연스럽고 편리한 단위입니다. 특히 삼각함수의 미분과 적분에서 라디안을 사용하면 간단한 형태로 나타낼 수 있습니다. 또한, 물리학에서는 각속도, 각가속도 등을 표현할 때 라디안을 사용하는 것이 일반적입니다.
라디안과 도는 각도를 나타내는 서로 다른 단위이지만, 상황에 따라 적절한 단위를 선택하여 사용해야 합니다. 수학적인 계산이나 물리학적인 문제를 풀 때는 라디안을 사용하는 것이 일반적이며, 일상생활에서는 도를 사용하는 것이 더욱 직관적일 수 있습니다.
스테라디안: 3차원 공간에서의 각도
스테라디안(steradian)이란?스테라디안(steradian)은 3차원 공간에서 어떤 점을 중심으로 펼쳐진 공간의 크기를 나타내는 단위입니다. 마치 평면에서 각도를 라디안으로 측정하듯, 입체적인 공간에서
engineer-daddy.co.kr
'Learn > 과학공학기술' 카테고리의 다른 글
| 브레트 법칙: 유기화학의 기본 원리와 새로운 가능성 (0) | 2024.11.04 |
|---|---|
| 스테라디안: 3차원 공간에서의 각도 (0) | 2024.11.02 |
| 광학 두께(광학적 깊이, Optical depth)의 의미와 중요성 (0) | 2024.10.22 |
| 달의 같은 면만 보이는 이유: 조석고정(Tidal Locking) 쉽게 설명 (1) | 2024.10.17 |
| 파이로프로세싱과 소듐냉각고속로의 결합 (0) | 2024.09.15 |



